

Before you get started, take this readiness quiz.
Just like a linear equation in one variable is an equation that is equivalent to (a linear expression\(=0\)), a quadratic equation is an equation in one variable, is an equation that is equivalent to (\(\text=0\)), and the equation isn't equivalent to a linear equation. For example, suppose that the area of a rectangular region with the length 3 feet more than twice its width (in feet) is equal to a square region of the twice the width of the other. We don't know what the width is (let's call it \(w\)) but we can write down this assertion about the width.
If the length of the rectangular region is 3 more than twice its width,
then its length is
Now, this looks like a quadratic equation, at least on the surface, but we need to make sure it isn't a linear equation in disguise so we subtract \(4w^2\) from both sides of the equation to get
We will not show this in detail, but an equation of the form \(0=\)(something quadratic) is not a linear equation.
This is the assertion about the width in the problem! Whatever \(w\) is, it satisfies the equation
For example, \(w\not= 1\) since if it were, \(-2w^2+3w=-2 (1)^2+3(1)=1\) which is not \(0\) as asserted.
Our question is then, how do you find the width (so that if you substitute that width in for \(w\) the assertion is true!
In general we will be interested in finding the solutions to quadratic equations.
A solution to an equation in a variable (lets call it \(x\)) is a number that we can substitute in for \(x\) that makes the equation true.
Two equations are equivalent if they have the same solutions.
A quadratic equation with one variable, say, \(x\), has polynomials on both sides of the equation and can be written in standard form : \(Ax^2+Bx+C=0\) where \(A\) is not zero, i.e., there is an equivalent equation of the form \(Ax^2+Bx+C=0\).
It is important to understand the difference between expressions and equations. We give here examples to demonstrate the two concepts.
A quadratic expression and a quadratic equation are not the same types of objects. Here are some examples.
| Expressions | Equation |
| \(2x+1\), \(0\) | \(2x+1=0\) (linear equation) |
| \(x^2\), \(x-2\) | \(x^2=x-2\) (quadratic equation) |
| \(3x^2+5x-1\), \(0\) | \(3x^2+5x-1=0\) (quadratic equation) |
Note that \(x^2+5x=x(x+5)\) is not a polynomial equation that we aim to solve. This is an identity of polynomials that was developed in the process of factoring out the GCF.
It does not make sense to "solve a polynomial." We can only solve equations. For example, we cannot solve \(2x+1\) as there is no statement to assess. Whereas \(2x+1=0\) is either true or false for a particular value of \(x\). Below we check whether or not some values of \(x\) are solutions to the equation \(2x+1=0\).
| \(\bf\) | True or False | Solution or Not a Solution |
| \(5\) | \(2\cdot 5 + 1= 0\) is false | Not a Solution |
| \(0\) | \(2\cdot 0 +1 = 0\) is false | Not a Solution |
| \(-\dfrac\) | \(2\cdot \left(-\dfrac\right) +1 = 0\) is true | Solution |
To solve quadratic equations we need methods different from the ones we used in solving linear equations. We will look at one method here and then several others in a later chapter.
Is \(x^3-2x+1=x^3+2x^2+x-7\) a quadratic equation? If so, is \(x=2\) a solution?
The left and the right sides of the equality are not quadratic, so the first impulse may be to say that this is not a quadratic equation. But let's be patient and see if we can put it in the required form:
We see that \(A\) is not zero, so this is indeed a quadratic equation.
To see whether \(2\) is a solution, we can substitute it into any of the equivalent equations to check it's truth. We'll check to see if \(2\) is a solution to \(2x^2+3x-8=0\).
The left hand side is \(2(2)^2+3(2)-8=6\) which is not equal to the right hand side (\(0\)). So \(2\) is not a solution to the equation!
We could've checked the original equation instead and arrived at the same conclusion.
Finding solutions to a quadratic equation is, in general, a little more difficult than finding solution to a linear equation. But we know that we can sometimes write a quadratic equation as a product of two linear factors (or two linear expressions and a number). As we will see this can be vary handy!!
We know that \(a\cdot 0=0\) and \(0\cdot a=0\) no matter what \(a\) is. Suppose though that \(a\cdot b =0\). What does this tell us about \(a\) and \(b\)?
Either \(a=0\) or it is not.
If \(a\not= 0\), then we can divide both sides of the equality by \(a\).
This is called the zero product property:
If \(ab=0\) then \(a=0\) or \(b=0\) or both.
This property will allow us to sometimes solve quadratic equations by reducing the problem to something we already know how to do, namely, solve linear equations.
We have seen that it is sometimes the case that we can write a quadratic expression as a product of two linear expressions. If we know this product is zero, then we can use the zero-product property!
We start with an example,
Lets solve \((2x-3)\cdot (3x+5)=0\).
Solution
If the equation is true, then this asserts something about the unknown which we call \(x\). This equation is a product of numbers (that we don't know) and that product is zero. So we can use the zero-product property to conclude that
either \((2x-3)=0\) or \((3x+5)=0\) (or both).
In other words, if \((2x-3)\cdot (3x+5)=0\) is true about \(x\), then either \((2x-3)=0\) is true or \(3x+5)=0\) is true (or both).
We have experience solving these linear equation from the last section!
If \((2x-3)=0\) then \(2x-3+3=0+3\), or, \(2x=3\). \(x\) is still being multiplied by \(2\) so we must divide both sides of the equal sign by \(2\)
\(2x/2=3/2\) or, simplifying, \(x=3/2\).
Similarly, if \(3x+5)=0\) then \(x=-5/3.\)
To conclude, if \((2x-3)\cdot (3x+5)=0\) then it must be that either \(x=3/2\) or \(x=-5/3\).
So, we have solved the equation by finding the values that when substituted in for \(x\) yield a true statement, namely, \(3/2\) and \(-5/3\).
In the context of an application, we may have more information about \(x\) that will help us pin down our unknown to one single answer.
Answer
Answer
The Zero Product Property works very nicely to solve quadratic equations. The quadratic equation must be factored, with zero isolated on one side. So be sure to start with the quadratic equation in standard form, \(ax^2+bx+c=0\). Then factor the expression on the left.
Solution

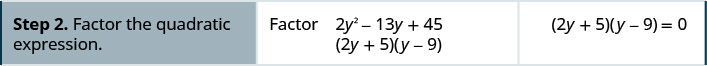


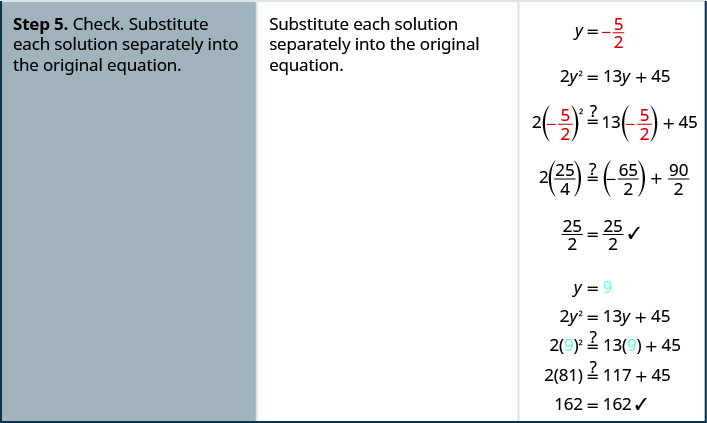
Answer
Answer
Before we factor, we must make sure the quadratic equation is in standard form.
Solving quadratic equations by factoring will make use of all the factoring techniques we have learned in this chapter! Do we recognize the special product pattern in the next example?
Answer
Answer
In the next example, the left side of the equation is factored, but the right side is not zero. In order to use the Zero Product Property, one side of the equation must be zero. We’ll multiply the factors and then write the equation in standard form.
Answer
Answer
In the next example, when we factor the quadratic equation we will get three factors. However the first factor is a constant. We know that factor cannot equal 0.
Solution
Answer
Answer
The Zero Product Property also applies to the product of three or more factors. If the product is zero, at least one of the factors must be zero. We can solve some equations of degree greater than two by using the Zero Product Property, just like we solved quadratic equations.
Solution
Answer
Answer
We will now continue with our application:
Suppose that the area of a rectangular region with the length 3 feet more than twice its width (in feet) is equal to a square region twice the width of the other. Find the dimensions of the two regions.
Solution
We saw in the introduction that if we call the width \(w\), that the length is then \(2w+3\) and the assertion is
which is equivalent to
So, let's factor this so that it looks more like our previous example (which we now know how to go about solving).
We have experience factoring from Unit 1, but we will remind you to factor out the GCF which is \(w\).
An equivalent equation is therefore
Again, this is an assertion about the width, i.e., the width \(w\) that we are looking for is a solution to this equation. Using the zero-product property we see that
if \(w(-2w+3)=0\) then \(w=0\) or \(-2w+3=0\)
if \(w(-2w+3)=0\) then \(w=0\) or \(w=3/2\).
Since \(w\) is a width, we see that it doesn't make sense for \(w\) to be zero. So, \(w\) must be 3/2.
The length of the rectangle is then \(2(3/2)+3=6\) feet. So the rectangle is 6 ft by 3/2 ft and the square is 3 ft by 3 ft. (we can see that the areas of both regions is 9 sq ft).
The product of two consecutive odd integers is 323. Find the integers.
The product of two consecutive odd integers is 255. Find the integers.
Answer
The product of two consecutive odd integers is 483 Find the integers.
Answer
Were you surprised by the pair of negative integers that is one of the solutions to the previous example? The product of the two positive integers and the product of the two negative integers both give positive results.
In some applications, negative solutions will result from the algebra, but will not be realistic for the situation.
A rectangular bedroom has an area 117 square feet. The length of the bedroom is four feet more than the width. Find the length and width of the bedroom.
| Step 1. Read the problem. In problems involving geometric figures, a sketch can help you visualize the situation. | 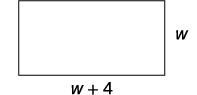 |
| Step 2. Identify what you are looking for. | We are looking for the length and width. |
| Step 3. Name what you are looking for. | Let \(w=\text< the width of the bedroom>\). |
| The length is four feet more than the width. | \(w+4=\text< the length of the garden>\) |
| Step 4. Translate into an equation. | |
| Restate the important information in a sentence. | The area of the bedroom is 117 square feet. |
| Use the formula for the area of a rectangle. | \(A=l·w\) |
| Substitute in the variables. | \(117=(w+4)w\) |
| Step 5. Solve the equation Distribute first. | \(117=w^2+4w\) |
| Get zero on one side. | \(117=w^2+4w\) |
| Factor the trinomial. | \(0=w^2+4w−117\) |
| Use the Zero Product Property. | \(0=(w^2+13)(w−9)\) |
| Solve each equation. | \(0=w+13\quad 0=w−9\) |
| Since \(w\) is the width of the bedroom, it does not make sense for it to be negative. We eliminate that value for \(w\). | \(\cancel\) \(\quad w=9\) |
| \(w=9\) The width is 9 feet. | |
| Find the value of the length. | \(w+4\) \(9+4\) 13 The length is 13 feet. |
| Step 6. Check the answer. Does the answer make sense? |
A rectangular sign has area 30 square feet. The length of the sign is one foot more than the width. Find the length and width of the sign.
Answer
The width is 5 feet and length is 6 feet.
A rectangular patio has area 180 square feet. The width of the patio is three feet less than the length. Find the length and width of the patio.
Answer
The length of the patio is 12 feet and the width 15 feet.
In the next example, we will use the Pythagorean Theorem \((a^2+b^2=c^2)\). This formula gives the relation between the legs and the hypotenuse of a right triangle.
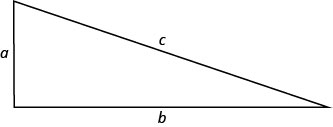
We will use this formula to in the next example.
A boat’s sail is in the shape of a right triangle as shown. The hypotenuse will be 17 feet long. The length of one side will be 7 feet less than the length of the other side. Find the lengths of the sides of the sail.
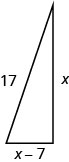
| Step 1. Read the problem | |
| Step 2. Identify what you are looking for. | We are looking for the lengths of the sides of the sail. |
| Step 3. Name what you are looking for. One side is 7 less than the other. | Let \(x=\text< length of a side of the sail>\). \(x−7=\text< length of other side>\) |
| Step 4. Translate into an equation. Since this is a right triangle we can use the Pythagorean Theorem. | \(a^2+b^2=c^2\) |
| Substitute in the variables. | \(x^2+(x−7)^2=17^2\) |
| Step 5. Solve the equation Simplify. | \(x^2+x^2−14x+49=289\) |
| \(2x^2−14x+49=289\) | |
| It is a quadratic equation, so get zero on one side. | \(2x^2−14x−240=0\) |
| Factor the greatest common factor. | \(2(x^2−7x−120)=0\) |
| Factor the trinomial. | \(2(x−15)(x+8)=0\) |
| Use the Zero Product Property. | \(2\neq 0\quad x−15=0\quad x+8=0\) |
| Solve. | \(2\neq 0\quad x=15\quad x=−8\) |
| Since \(x\) is a side of the triangle, \(x=−8\) does not make sense. | \(2\neq 0\quad x=15\quad \cancel\) |
| Find the length of the other side. | |
| If the length of one side is then the length of the other side is |    8 is the length of the other side. |
| Step 6. Check the answer in the problem Do these numbers make sense? |
Justine wants to put a deck in the corner of her backyard in the shape of a right triangle. The length of one side of the deck is 7 feet more than the other side. The hypotenuse is 13. Find the lengths of the two sides of the deck.
Answer
5 feet and 12 feet
A meditation garden is in the shape of a right triangle, with one leg 7 feet. The length of the hypotenuse is one more than the length of the other leg. Find the lengths of the hypotenuse and the other leg.
Answer
24 feet and 25 feet
Solve the equation \(x(x+1)=−x+35\) by using the Zero Product Property.